树和二叉树、二叉堆

• 树
  • 树是由结点和边组成的，自顶而下，不存在环的一种数据结构。
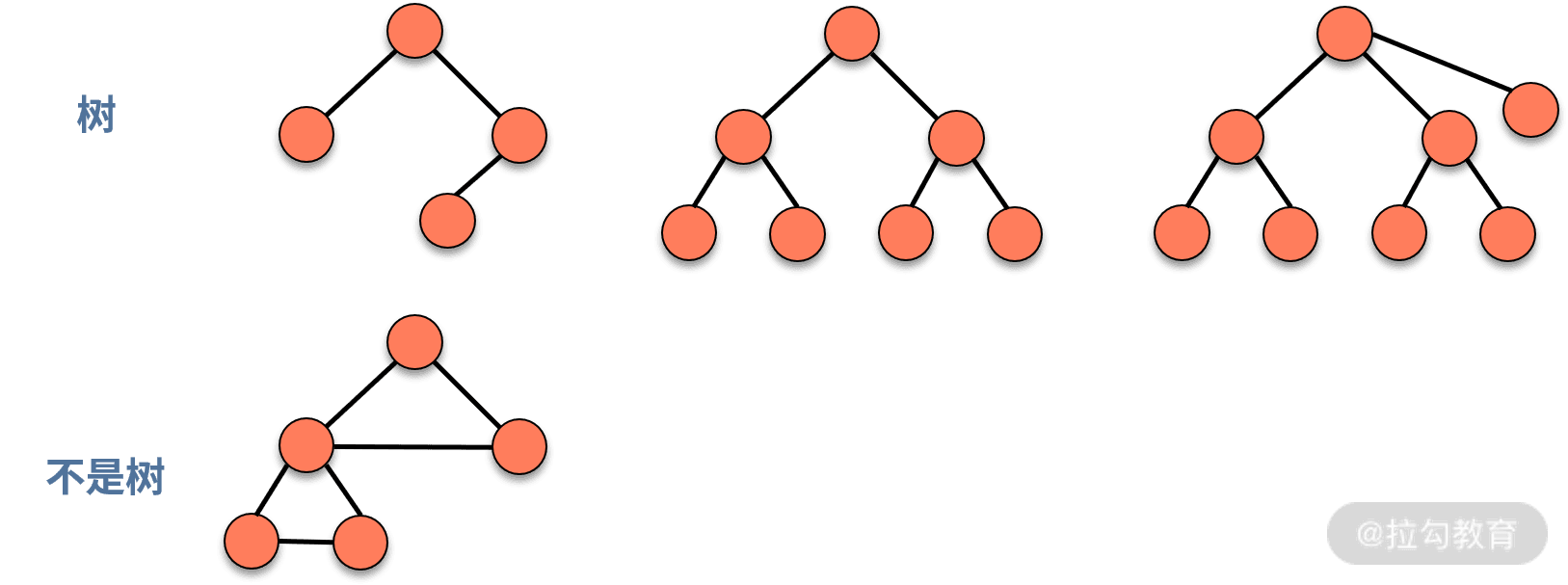
  • 特性：根、子节点、深度（树中结点的最大层次数，就是这棵树的树深）
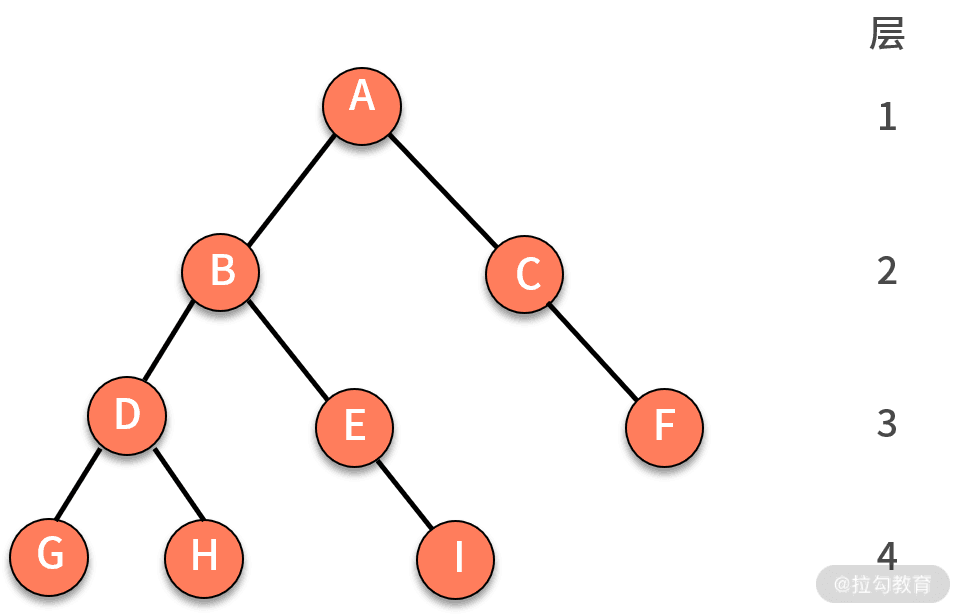
  • 树的遍历
    • DFS：前序遍历、中序遍历、后序遍历：节点的处理位置不同

      function traverse(TreeNode root) {
          if (root == null) {
              return;
          }
      
          // 前序遍历代码位置
          traverse(root.left);
          // 中序遍历代码位置
          traverse(root.right);
          // 后序遍历代码位置
      }
      

      Copy to clipboard
    • BFS：层序遍历

      let queue = [root]
      while (queue.length) {
          let node = queue.shift()
          let [left, right] = node
      
          if(left) {
            queue.push(left)
          }
      
          if(right) {
            queue.push(right)
          }
      }
      

      Copy to clipboard
  • 二叉树、满二叉树、完全二叉树、二叉搜索树
  • 二叉搜索树
    • 左子树中的每个结点的值都小于父结点
    • 右子树中的每个结点的值都大于父结点
    • 左右子树同样也是一个二叉搜索树
    • 对二叉查找树进行中序遍历，就可以输出一个从小到大的有序数据队列
• 普通二叉树复杂度 O(n)；二叉查找树应用了二分查找的思想，复杂度则是 O(logn)
  • 平衡二叉搜索树：当二叉树节点分布不均匀时，会极大影响数据查询的性能，所以为了保证数据的均衡性，就有了平衡二叉树的结构。平衡二叉树采用平衡算法可以让数据均匀的分布到树里的各个节点，避免树的高度相差太多，从而解决二叉树的层级不稳定问题
    • 特点：
    • 应用
      • 红黑树
      • AVL树
• 堆

二叉树、满二叉树、完全二叉树、二叉搜索树

• 二叉树：每个结点最多有两个子结点，分别称作左子结点和右子结点。
• 满二叉树：只有最后一层无任何子结点，其他所有层上的所有结点都有两个子结点的二叉树。

完全二叉树

除了最后一层以外，其他层的结点个数都达到最大，并且最后一层的叶子结点都靠左排列。

完全二叉树的由来，主要是跟“非完全二叉树”的树结构以及对应的存储结构做对比

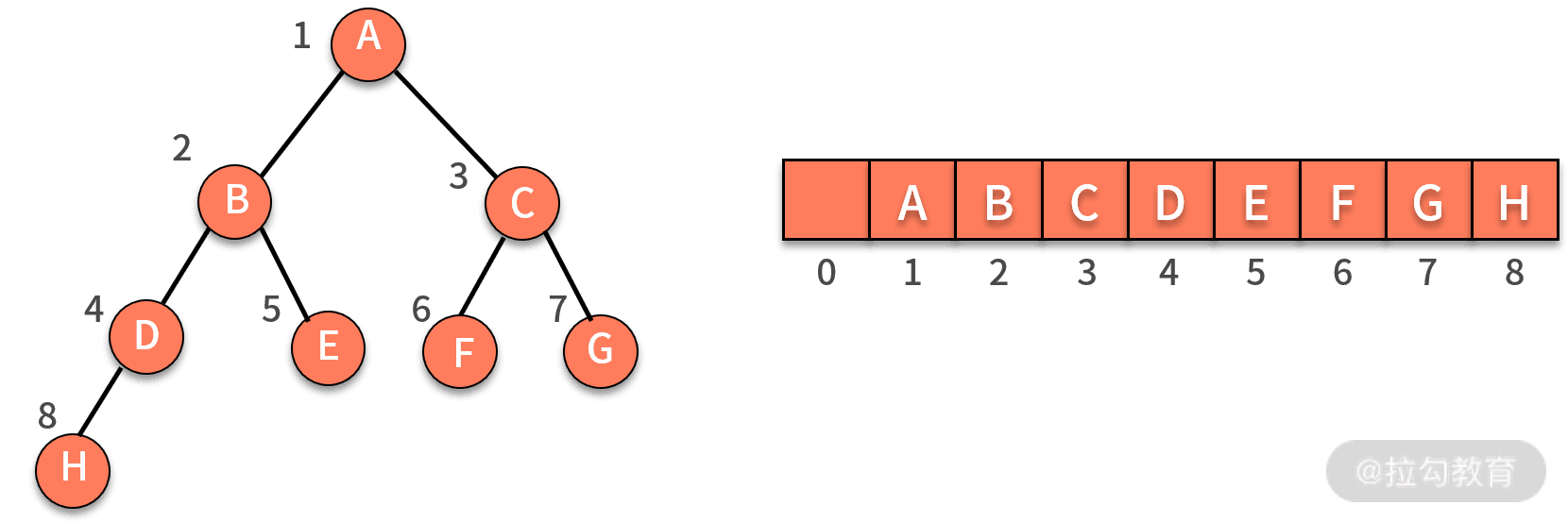
完全二叉树上节点对应的索引刚好可以完全落应在数组上。

为了方便计算，i 从 1 开始。结构特点：

• 索引为i的左孩子的索引是 2i
• 索引为i的左孩子的索引是 2i+1
• 索引为i的父结点的索引是 Math.floor(i/2)

非完全二叉树

非完全二叉树，树的中间结构上是不完全的，导致在数组上存储是有浪费的。

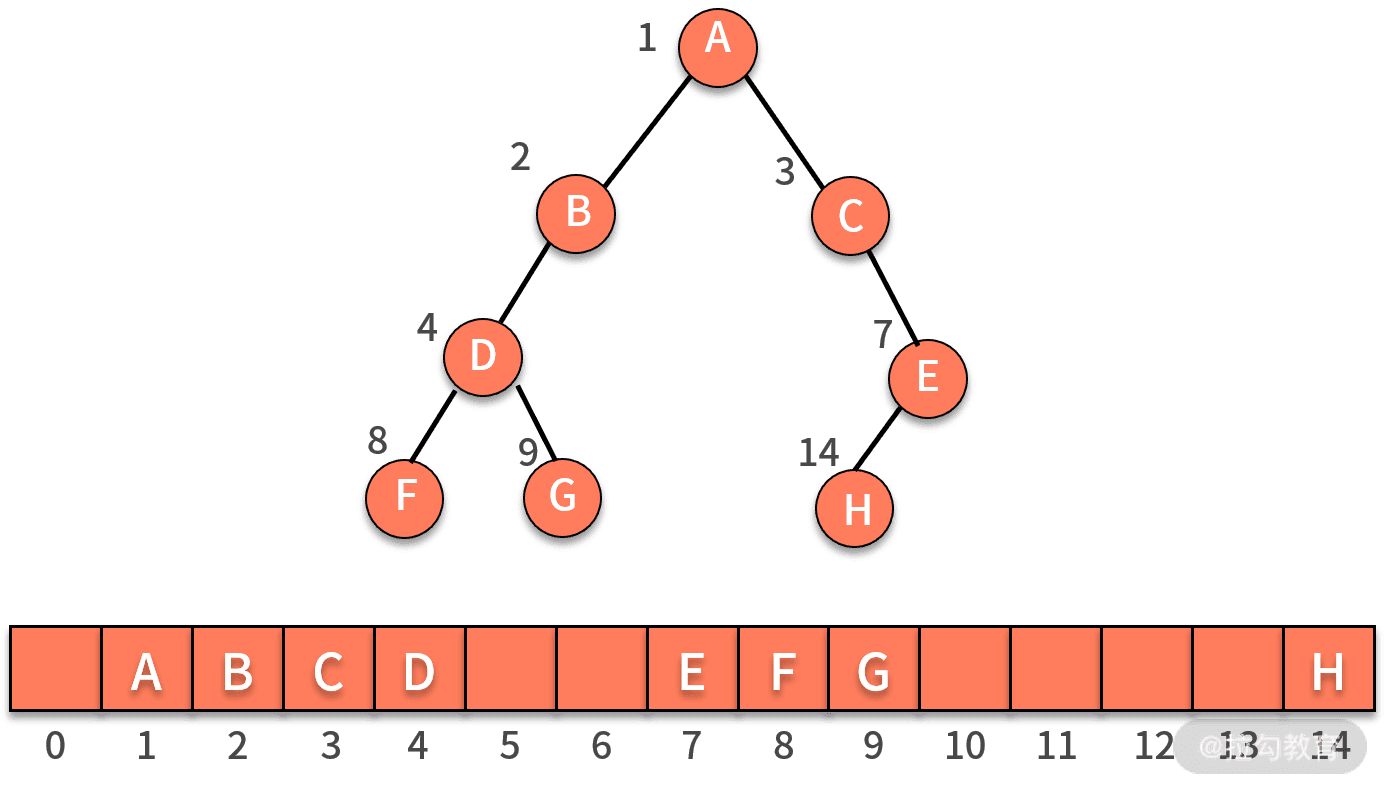
堆

堆是一种特殊的基于树的数据结构，一种称为优先队列的抽象数据类型。
堆分为「大顶堆」和「小顶堆」，大（小）顶堆：任意节点的值不大于（小于）其父节点的值。

优先级队列是一种特殊的队列，优先级高的数据先出队，而不再像普通的队列那样，先进先出

堆和树有什么区别？堆为什么要叫堆，不叫树呢？ - Severus的回答 - 知乎

堆的常见实现是二叉堆：基于完全二叉树性质的数据结构，使用数组存储：

• 易于存储、索引，不会造成空间浪费
• 平衡层级，堆化过程保持在 O(logn)：一个包含 n 个节点的完全二叉树，树的高度不会超过 log ​n。堆化的过程是顺着节点所在路径比较交换的，所以堆化的时间复杂度跟树的高度成正比，也就是 O(logn)。插入数据和删除堆顶元素的主要逻辑就是堆化，所以，往堆中插入一个元素和删除堆顶元素的时间复杂度都是 O(logn)

js 二叉堆实现

堆应用：

• 堆排序
• Top K 问题

  建堆后，如果元素比堆顶元素大，我们就把堆顶元素删除，并且将这个元素插入到堆中；如果比堆顶元素小，则不做处理。

• 中位数

  1. 排序后分成两部分前后分别为大、小顶堆，大顶堆顶部元素即为中位数
  2. 如果新加入的数据小于等于大顶堆的堆顶元素，我们就将这个新数据插入到大顶堆；否则，我们就将这个新数据插入到小顶堆。
  3. 堆调整
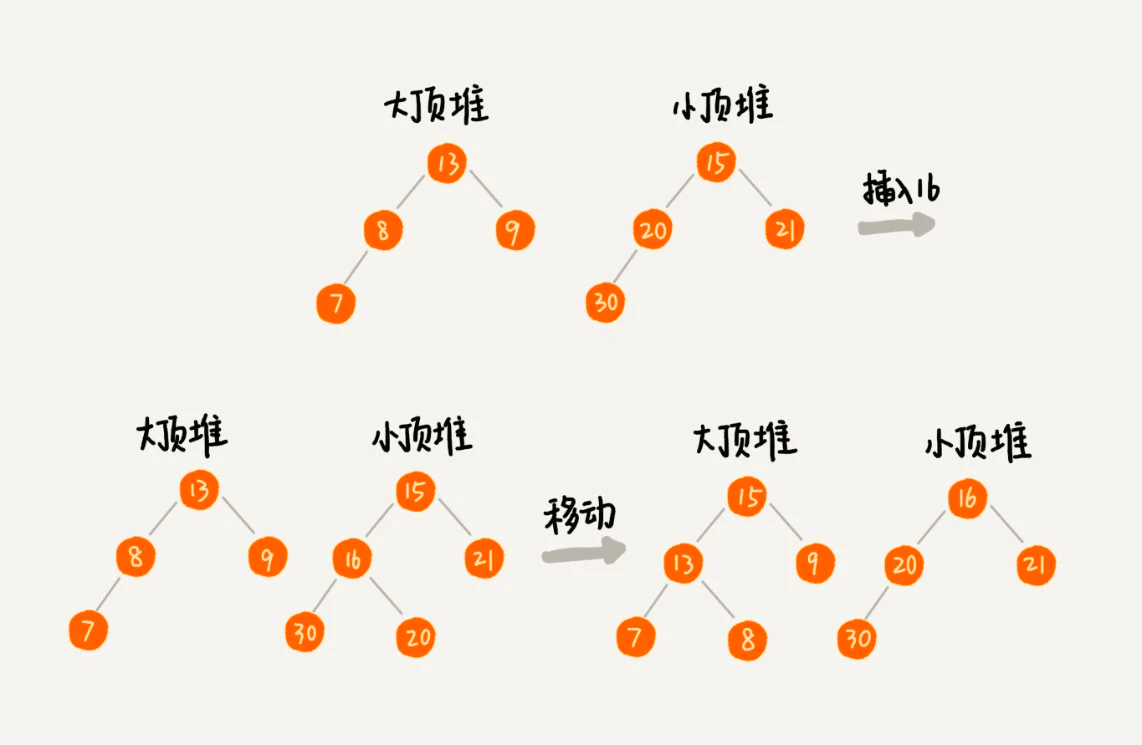
     保证大顶堆的数量为奇（偶）数，小顶堆为偶数