递归、分治、枚举、回溯、贪心、动态规划
递归
- 递归是一种应用非常广泛的编程技巧,本质上也是一种循环:通过函数体进行自我调用
- 递归模板
function recursion(level, param1, param2, ...) { // 1. 终止条件 // 2. 递归缓存(可选) // 3. 逻辑处理 // 4. 递归调用 // 5. 状态重置(可选) } - 递归终止条件
- 注意
- 每次函数调用都会产生开销,因此递归通常比迭代更加耗费内存空间,效率更低
- 内存栈溢出
- 重复计算
- 递归转迭代:模拟栈
- 尾递归:如果函数在返回前的最后一步才进行递归调用,则该函数可以被编译器或解释器优化,使其在空间效率上与迭代相当。这种情况被称为「尾递归 tail recursion」
- 普通递归:当函数返回到上一层级的函数后,需要继续执行代码,因此系统需要保存上一层调用的上下文。
- 尾递归:递归调用是函数返回前的最后一个操作,这意味着函数返回到上一层级后,无须继续执行其他操作,因此系统无须保存上一层函数的上下文
- 递归模板
- 抵制人肉递归:计算机擅长做重复的事情,所以递归正合它的胃口。而我们人脑更喜欢平铺直叙的思维方式。当我们看到递归时,我们总想把递归平铺展开,脑子里就会循环,一层一层往下调,然后再一层一层返回,试图想搞清楚计算机每一步都是怎么执行的,这样就很容易被绕进去
分治
- 分治算法
- 分治,即分而治之
- 分治算法通常基于递归实现,“分、治”过程也正好和“递、归”
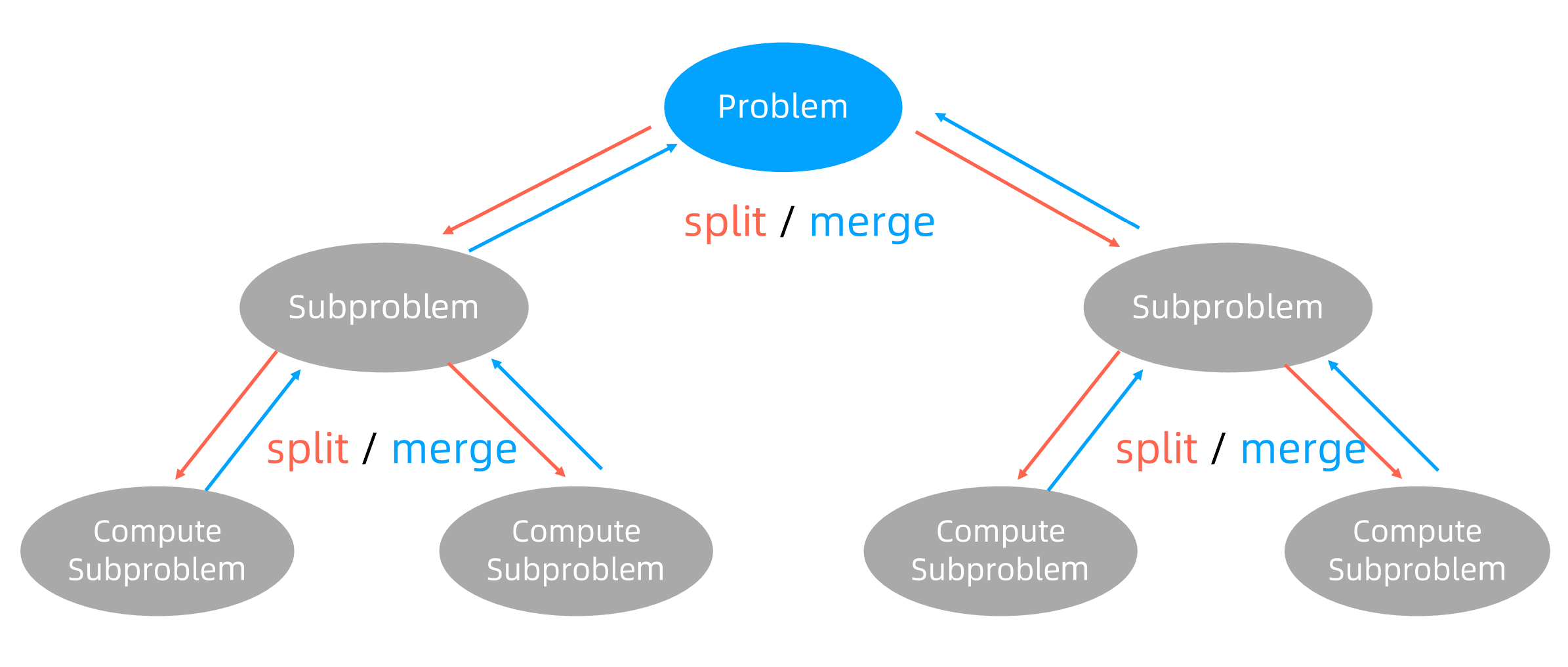
- 分(划分阶段):将原问题划分成 n 个规模较小,并且结构与原问题相似的子问题,如果分割后的问题仍然无法直接解决,那么就继续递归子问题,直到每个小问题都可解为止
- 治(合并阶段):至底向上合并每个子问题的结果,直到到原问题的解
- 分治效率:分治思想更多的是一种“拆分”问题的解决思路 🤔。而其分治法模型未必就高效,关键在于子问题的优化处理上,否则就起不到减小算法总体复杂度的效果了
- 操作数量优化
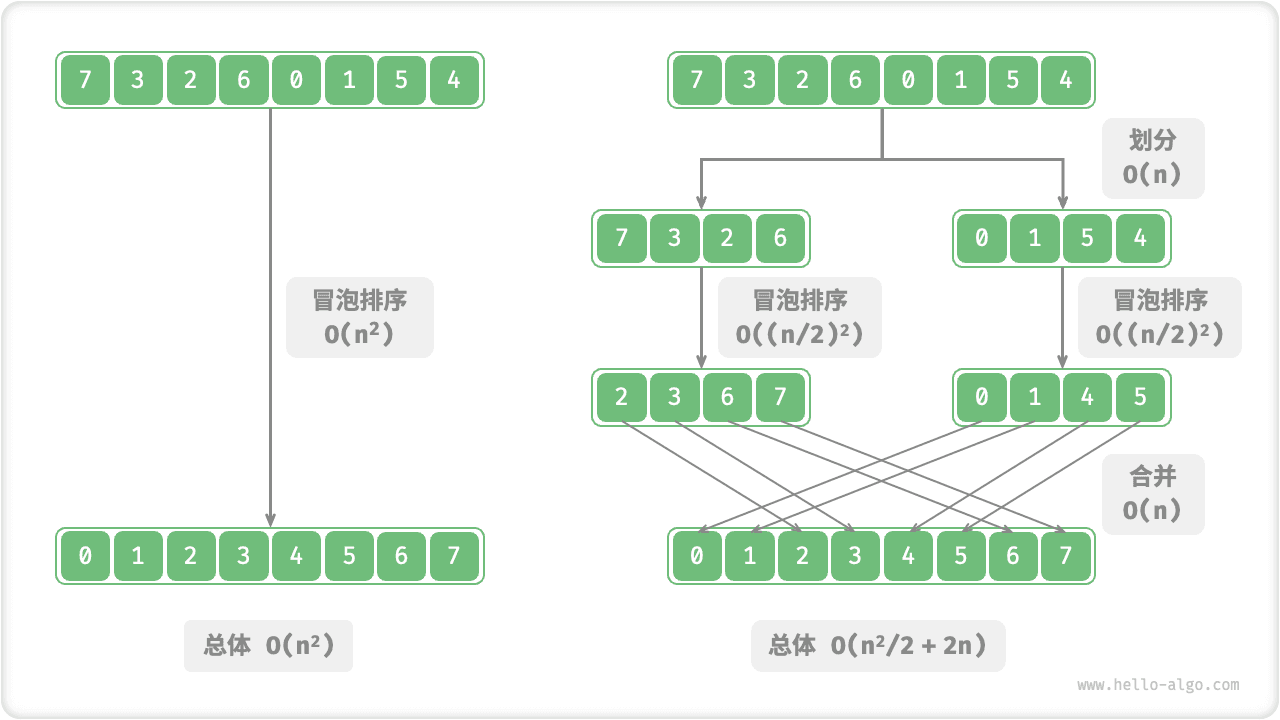
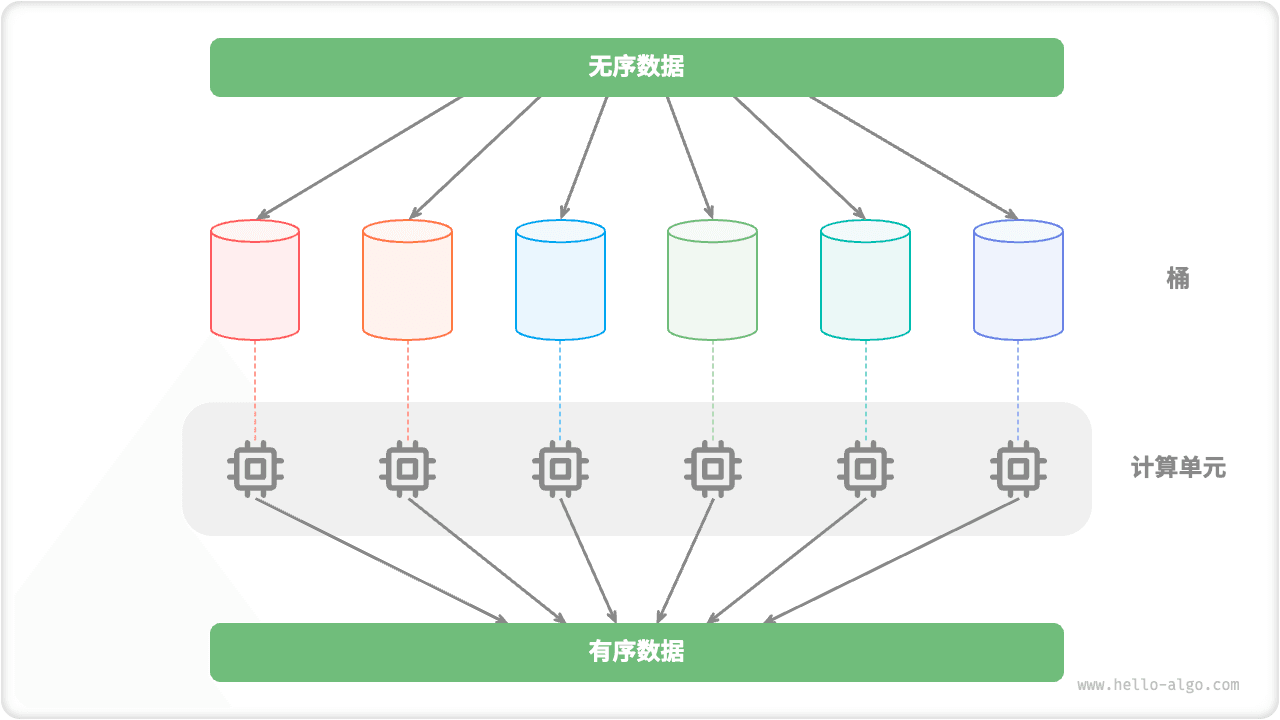
- 并行计算优化
- 操作数量优化
- 子问题独立性:分治法中原问题所分解出的各个子问题是相互独立的,没有重叠子问题即不包含重复数据,这一点是分治算法跟动态规划的明显区别
枚举、回溯、贪心、动态规划
leetcode 题目《零钱兑换》
给你一个整数数组 coins ,表示不同面额的硬币;以及一个整数 amount ,表示总金额。
计算并返回可以凑成总金额所需的最少的硬币个数 。如果没有任何一种硬币组合能组成总金额,返回 -1 。
输入:coins = [1, 2, 5], amount = 11
输出:3
解释:11 = 5 + 5 + 1
枚举
面对最值问题(求最大、最小、最优之类)的求解,本质上还是需要进行穷举,即直接暴力枚举所有的可能解,从所中选择满足条件的解。
回溯
回溯算法,一种采用试错思想在尝试和回退中穷举所有可能的解,并可通过剪枝避免不必要的搜索分支。
在这个过程中,分为多个阶段,每个阶段我们都会面对一个分岔路口,我们先随意选一条路尝试,当发现这条路走不通的时候(不符合期望的解),就回退到上一个岔路口,选择另选一种走法继续走。
回溯算法通常并不显式地对问题进行拆解,而是将问题看作一系列决策步骤。适合用回溯解决的问题通常满足决策树模型,这种问题可以使用树形结构来描述,其中每一个节点代表一个决策,每一条路径代表一个决策序列。
回溯算法通常采用“深度优先搜索”来遍历解空间,因为这种形式赋予了回溯这种可以回退一步的能力:它通过堆栈保存了上一步的当前状态。
针对上面题目,我们每次从 [1, 2, 5] 中选择出不同的数组合出刚好符合条件的结果。
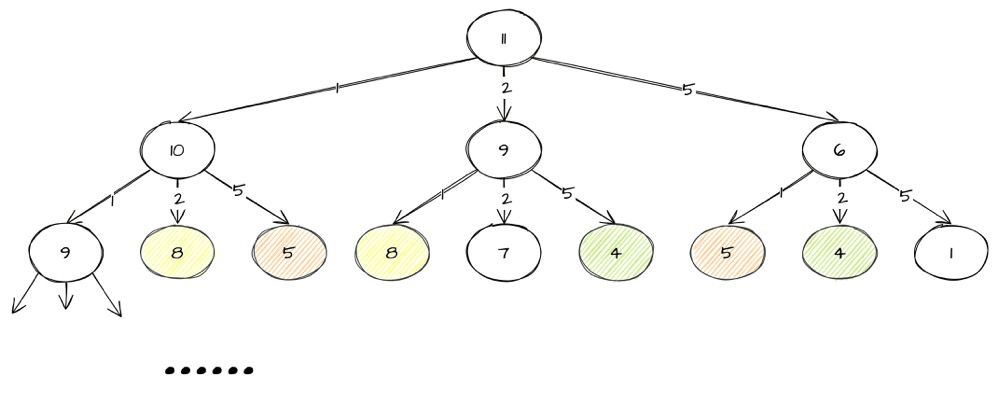
在这个过程中,我们不断构建解空间,一颗“状态”树,搜索接近问题状态的树。我们将问题转成树结构的思维模式,我们只需要对这颗状态树进行遍历即可。
回溯算法的框架:
// python 示例
result = []
def backtrack(路径, 选择列表, 结果):
if 满足结束条件:
结果.add(路径)
return
for 选择 in 选择列表:
做选择
backtrack(路径, 选择列表)
撤销选择,恢复到之前的状态
本题目用回溯解法如下:
var coinChange = function (coins, amount) {
const result = [];
dfs(coins, amount, result);
return Math.min(...result);
};
function dfs(coins, amount, result, target = 0, count = 0) {
if (target >= amount) {
return result.push(count);
}
for (const c of coins) {
dfs(coins, amount, result, target + c, count + 1);
}
}
回溯算法本质上是一种穷举,尝试所有可能的解决方案直到找到满足条件的解,时间复杂度可以达到指数级。不过在搜索过程可以使用剪枝优化,即剪去一些不可能到达最终状态(即答案状态)的节点,从而减少状态空间树节点的生成。常见剪枝优化操作有:
- 备忘录
- 可行性剪枝:当搜索到某个状态时,如果发现这个状态不能产生解,就可以剪去这个状态及其子树
- 最优性剪枝:当搜索到某个状态时,如果已经找到了一条更优的解,就可以剪去这个状态及其子树
- 启发式搜索:在搜索过程中引入一些策略或者估计值,从而优先搜索最有可能产生有效解的路径
动态规划
- 动态规划
- 动态规划是一种通过子问题分解来求解原问题的思路
动态规划是一种“从底至顶”的形式:从最小子问题的解开始,迭代地构建更大子问题的解,直至得到原问题的解
- 特征
- 重叠子问题:动态规划和分治算法同样是子问题分解的思路,但分治算法不能有重叠子问题。动态规划之所以高效,就是因为子问题是相互依赖,存在大量的重叠子问题可以进行缓存优化
- 动态规划常用来求解最优问题。通过子问题的最优解来推导出原问题的最优解,也就是最优子结构
- 无后效性:给定一个确定的状态,它的未来发展只与当前状态有关,而与当前状态过去所经历过的所有状态无关。也就是说状态的决策转移不受过去状态的影响
- 多阶段决策最优解模型
- 动态规划原意是一种解决多阶段决策过程最优化问题的数学方法
- “阶段”意味着每个阶段都会产生多个状态,一个阶段的一个状态可以得到下个阶段的某几个状态,而下个阶段的某个状态可以由上个阶段的某些状态得到。这样我们把原问题拆分成多个子阶段问题,某个阶段的子问题只能由前面阶段更小的子问题的解得到
- 通过对阶段状态的优化来得到全局最优
- 思路
- 定义问题状态:思考如何将这个问题表达成状态,比如当问题状态 x 条件下,求问题结果 f(x)
- 寻找决策,得出状态转移方程
决策:能让状态发生变化的选择
- 状态转移
- 自顶向下模型:记忆化递归
- 自底向上模型:定义 dp 表,从初识状态转移填表,从最小子问题的解开始,迭代地构建更大子问题的解,直至得到原问题的解
- 动态规划是一种通过子问题分解来求解原问题的思路
题目的状态转移方程如下:
f(n) = Math.min(f(n - 1), f(n - 2), f(n - 5)) + 1
递归写法:
var coinChange = function (coins, amount) {
return dfs(coins, amount, 0);
};
var temp = {};
function dfs(coins, amount, level = 0) {
if (amount === 0) return level;
if (temp[amount]) return temp[amount];
let min = Infinity;
for (const c of coins) {
let _amount = amount - c;
if (_amount >= 0) {
temp[amount] = dfs(coins, _amount, level + 1);
min = Math.min(min, temp[amount]);
}
}
return min === Infinity ? -1 : min;
}
递推写法:
var coinChange = function (coins, amount) {
if (amount === 0) return 0;
let i = 1;
let temp = coins.reduce((obj, key) => ((obj[key] = 1), obj), {});
while (i <= amount) {
temp[i] ??= Math.min(...coins.map((c) => (temp[i - c] ??= Infinity))) + 1;
i++;
}
return temp[amount] === Infinity ? -1 : temp[amount];
};