底层存储结构:数组、链表
数据结构种类很多,它们存在的目的都是在不同的应用场景合理组织数据,尽可能高效地查找、修改,也就是更好的空间换时间策略。
但数据在计算机内存中的存储方式,可分为连续空间存储(数组)和分散空间存储(链表),所有数据结构都是基于数组、链表或二者的组合实现的。
- 数组
- 数组(Array)是用一组连续的内存空间,来存储一组具有相同类型的数据
- 由于是紧凑连续存储和相同数据类型的存储结构,所以数组可以随机访问,时间复杂度为 O(1),可以通过索引快速找到对应元素
- 但查询某个元素是否存在时需要遍历整个数组,耗费 O(n) 的时间
- 正因为连续存储,内存空间必须一次性分配够,所以说数组如果要扩容,需要重新分配一块更大的空间,再把数据全部复制过去,时间复杂度 O(N)
- 如果想要在数组中间进行插入和删除,每次必须搬移后面的所有数据以保持连续,时间复杂度 O(N)
- 数组访问越界
- 链表:是分散空间存储方式,通过指针将一组零散的内存块串联在一起,每个链表的结点除了存储数据之外还要额外存储指针
- 因为元素不连续,而是靠指针指向下一个元素的位置,所以不存在数组的扩容问题
- 如果知道某一元素的前驱和后驱,操作指针即可删除该元素或者插入新元素,时间复杂度 O(1)
- 插入:
x->next=c; b->next=x - 删除:
a->next=b->next 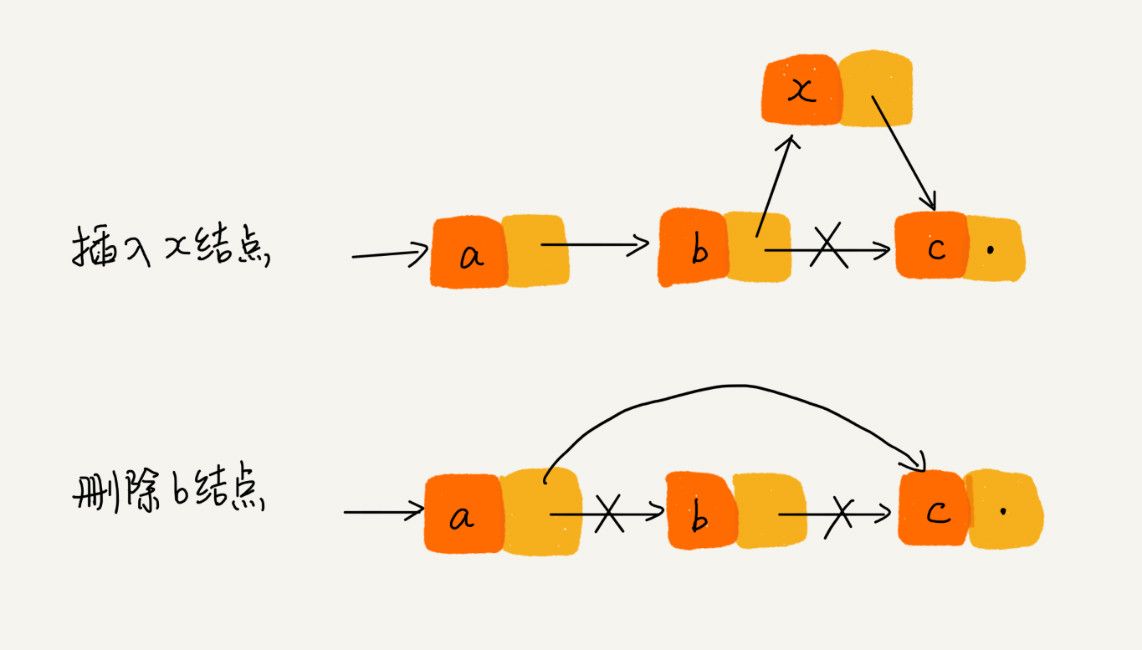
- 插入:
- 因为存储空间不连续,你无法根据一个索引算出对应元素的地址,所以不能随机访问,只能顺序访问,时间复杂度 O(n)
- 由于每个元素必须存储指向前或后元素位置的指针,会消耗相对更多的储存空间
- 链表类别
- 单链表
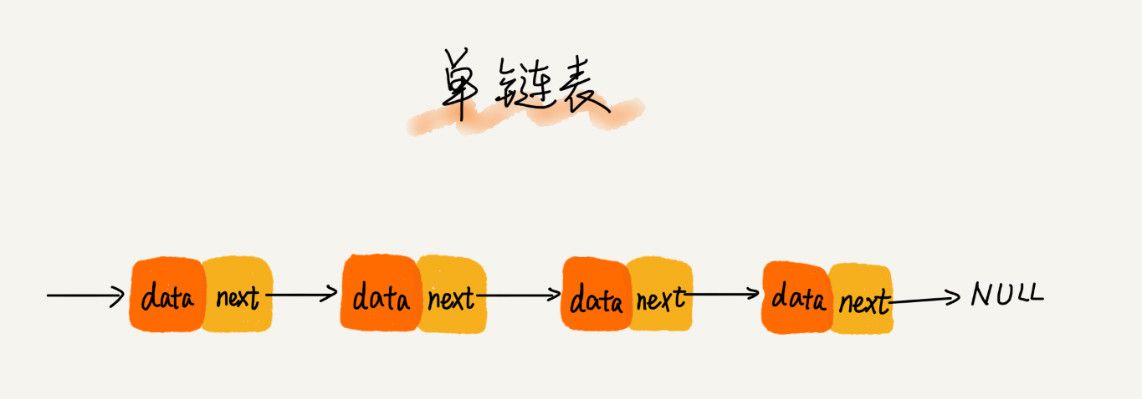
- 循环链表
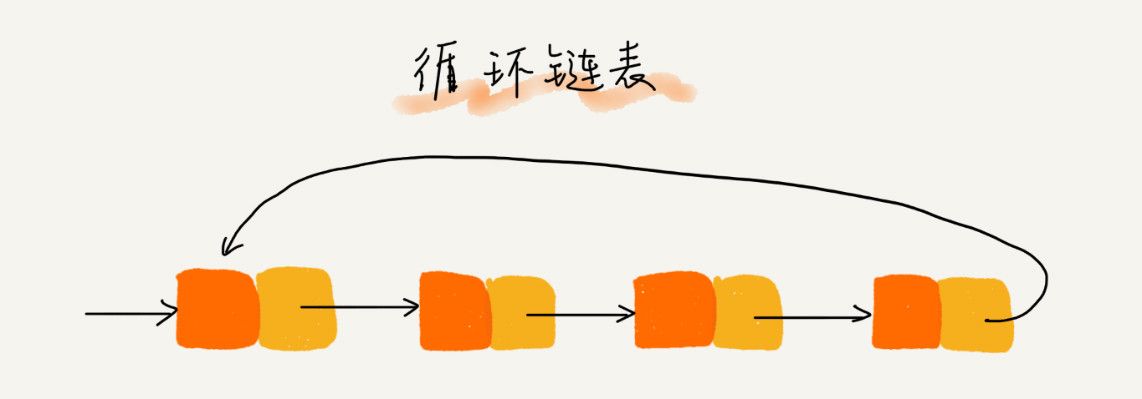
- 双向链表
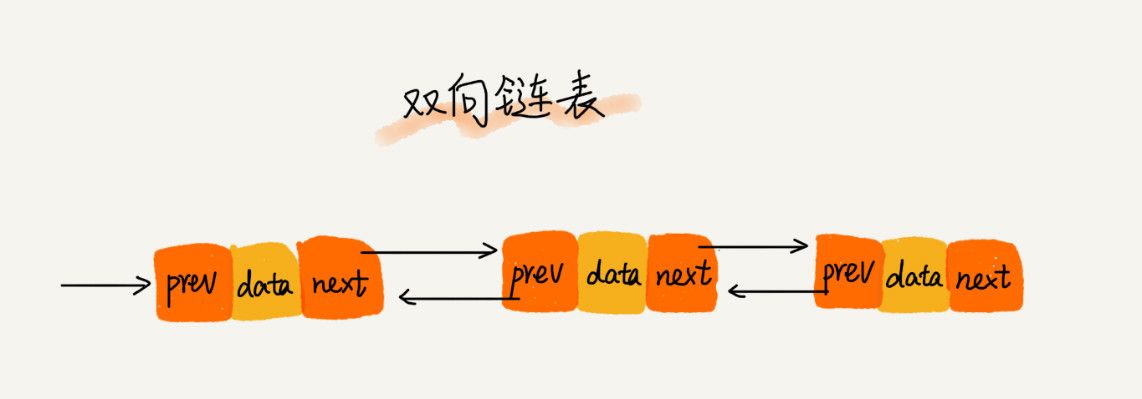
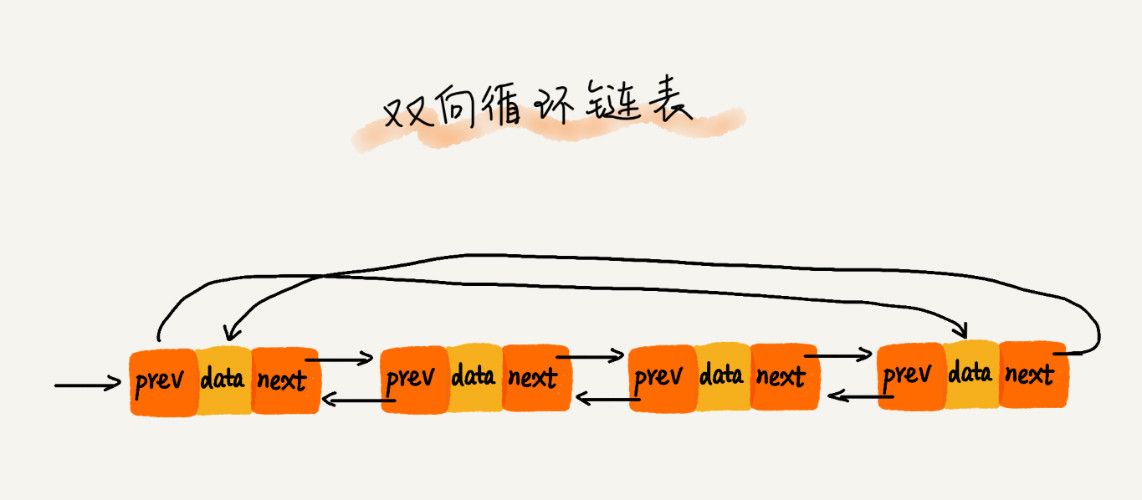
- 双向循环链表
- 单链表
- 链表技巧:使用带头链表防止空指针
- 使用带头链表:简化操作,针对链表的插入、删除操作,需要对插入第一个结点和删除最后一个结点的情况进行特殊处理
- 高级
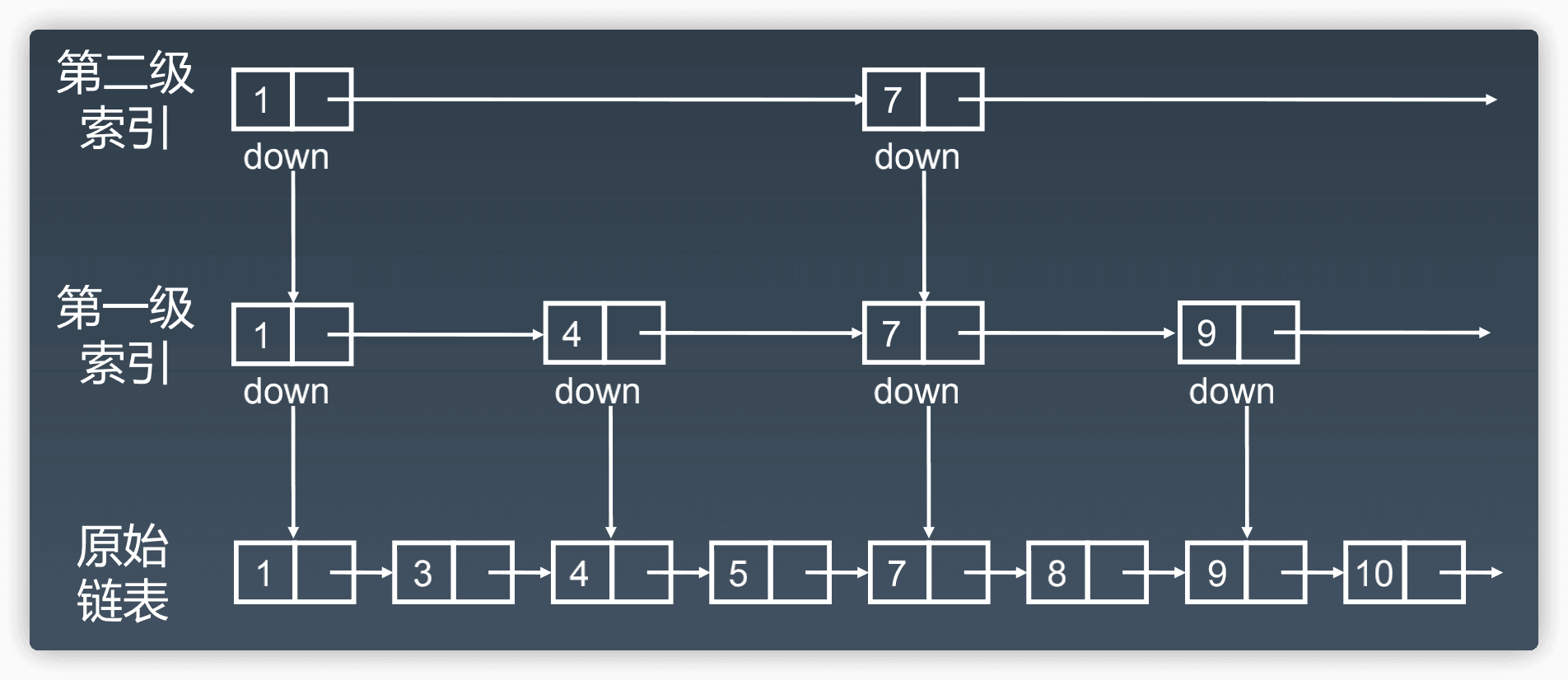
跳表
类似链表,查找操作如果需要加速,可以添加多级索引,变成跳表,以提升效率 思想推广一下就是,一维数据结构的某项操作如果需要加速,则可以进行升维,使其更多附加信息,以提升效率。 本质是空间换时间

其他文章
交流区
加载中...